What's Graph Theory?
Graph Theory is a powerful tool in computer science. It has nothing to do with "graphs" as the word is commonly used, but is rather a simple way of representing your data to allow you do a number of useful calculations.
The building blocks of Graph Theory are the vertex (also called a node) and the edge. Vertices (plural of vertex) tend to represent objects and edges typically represent the relationships between them.
Here is a sample (contrived) graph where the vertices are cities, and the edges are whether the city has an express flight between them.
As you can see, there is an express flight between Boston and New York and one between Atlanta and Miami, but there is not one between Boston and Atlanta.
One often-seen configuration of graphs have weighted edges. This means that each edge connecting two vertices has some value attached to it. Here's the express flight graph again, but this time each edge has the price of the express flight it represents attached to it as its weight.
This begins to suggest some of the usefulness of graphs; if this were a more accurate graph, you might use it to plot the cheapest way to move between two cities via express flights.
The two graphs we looked at so far have all had edges that were bidirectional. That is to say, the $49 edge between Chicago and New York meant that you could, for $49, fly from either Chicago to New York or from New York to Chicago. Of course, the world doesn't always work this way, and that's why we have directed graphs.
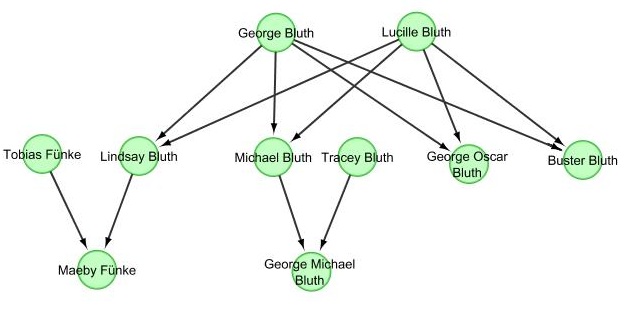
In a Directed Graph, the edges have a direction to them -- that is, instead of merely going between two vertices, they go from one vertex to another. Following is an example of a family tree, which is a kind of directed graph. In this case, an edge from one vertex to another vertex represents that the first vertex is a parent of the second.
Here you can see that George and Lucille Bluth are both parents to Michael Bluth, who is in turn a parent to George Michael Bluth.
Note that the lines representing the edges sometimes cross over each other -- that doesn't mean anything to the graph. Those intersections don't represent any actual connection and are just an inconvenience of trying to draw a graph on a 2-dimensional space.
While graph theory is simple in the small scale, they are important enough to have filled a library's worth of books on the topic. A large number of famous and important algorithms are within the realm of graph theory, and it's a powerful tool in any developer's arsenal.
I'll dive into further details (both more theory as well as implementation options) in future posts; please post any requests in the comments.
Further Reading
- Here! I intend to write more articles covering the basics of graph theory as well as interesting problems in it.
- Wikipedia's article on the topic gives a good high-level overview of the history, meaning, and current state of Graph theory.
- Introduction to Algorithms, Third Edition
is a classic book covering all algorithms, but spends over 150 pages covering many of the most important graph theory algorithms.
- Introduction to Graph Theory (2nd Edition)
is a wonderful graph theory text, but I'd recommend it only for those who have a sturdy footing in discrete math. The definitions, explanations and proofs are extremely rigorous and thorough, (though this sometimes comes at the expense of clarity).


No comments:
Post a Comment